In my opinion, the most important shape in maths is the circle. It’s so simple to understand, but it also gives us one of the most crucial constants in all of mathematics: p. Once we draw some lines inside a circle, we can deduce patterns and theorems that are useful both theoretically and in a practical sense. The defining feature of the circle is its constant radius, and I hope to show you that starting from this simple line, we can derive all the circle theorems you need to understand. Ready? Let’s go.
Firstly, we have to know how to construct an isosceles triangle from two radii. We’ll be doing this a lot, so here’s an example:
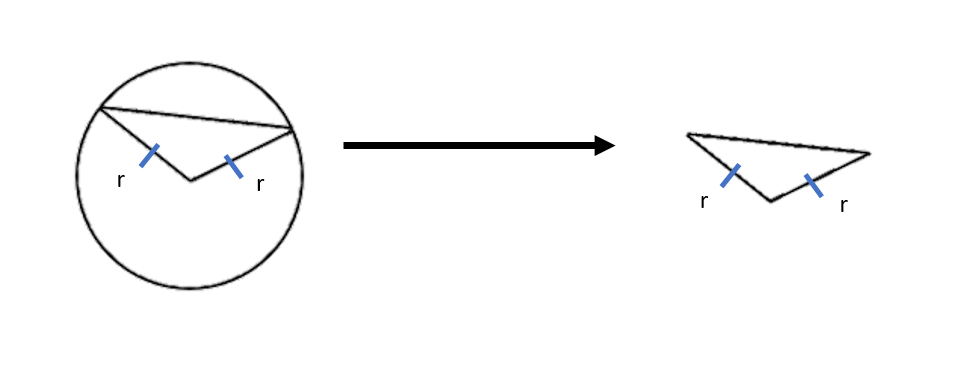
Since every radius is the same, drawing two radii forms a triangle with two equal sides – an isosceles triangle!
Now for the theorems:
1. The angle at the centre is twice the angle at the circumference
2. The angle in a semicircle is a right angle
3. Angles in the same segment are equal
4. Opposite angles in a cyclic quadrilateral sum to 180°
5. The angle between the chord and the tangent is equal to the angle in the alternate segment
Need help with your studies?
1. The angle at the centre is twice the angle at the circumference:
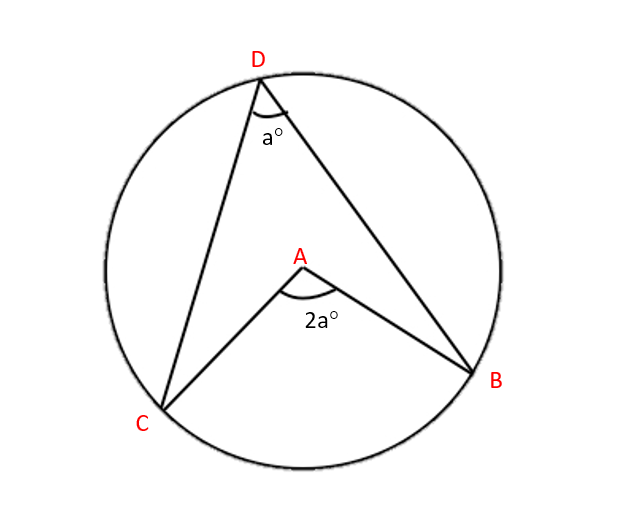

How do we show this? Start by drawing lines to connect A and D, and B and C. This forms three small triangles (∆ACD, ∆ABC, ∆ABD) and one big one (∆DCB). Since the lines AB, AC and AD are all radii of the circle, this means that the triangles ∆ACD, ∆ABD and ∆ABC are isosceles.
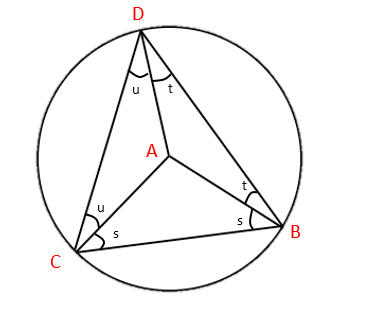

So we can see from ∆ABC that the angle at A is 180-2s (180° in a triangle).
And we have in the larger triangle ∆DCB that:
(u+s)+(u+t)+(t+s) = 180° (180° in a triangle).
which gives us:
2u+2t+2s = 180°
2u+2t = 180°-2s
= A
2. The angle in a semicircle is a right angle:
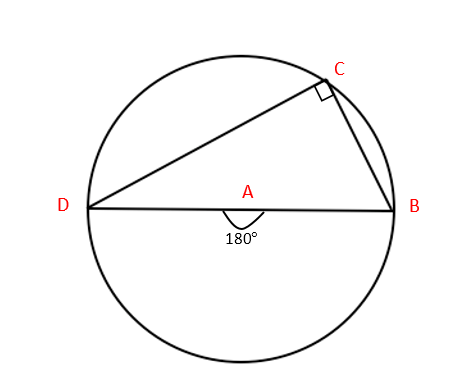

Firstly, we can see that this is an application of the theorem above, with angle at the centre = 180°. If we wanted to show this without using Theorem 1, start by drawing a line from A to C. Note that this is a radius of the circle. This makes three triangles: ∆ABC, ∆ACD and a large one, ∆BCD. We also have that ∆ABC and ∆ACD are isosceles.
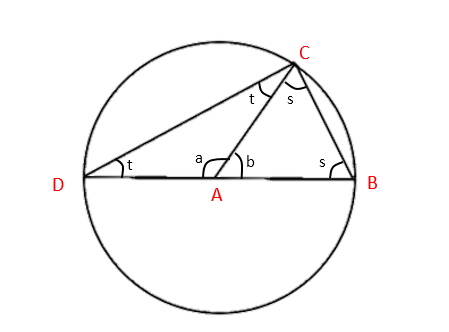

Firstly, we see that a+b=180° (180° on a straight line).
For ∆ABC, we can see that b+2s=180° (180° in a triangle). (1)
And for ∆ACD we have that a+2t=180° (180° in a triangle). (2)
If we add equations (1) and (2), we have b+2s+a+2t = 360°. We also know that a+b=180°. So:
2s+2t+180° = 360°
2s+2t = 180°
s+t = 90°, which is what we were after.
3. Angles in the same segment are equal:
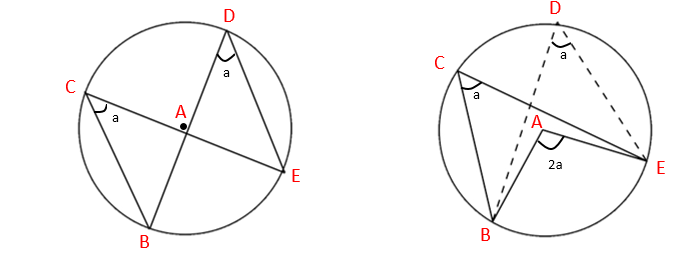

The way we show this is by using the first theorem. We can see that by applying the first theorem, we have that the angle at C is half the angle at A (the centre). We have that the angle at D is also half the angle at A. Therefore, the angle at C is equal to the angle at D.
4. Opposite angles in a cyclic quadrilateral sum to 180°:
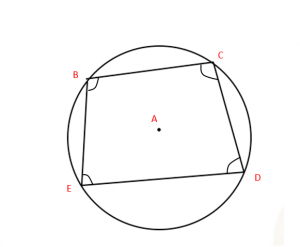

Angle at B + angle at D = angle at C + angle at E = 180°
A cyclic quadrilateral is a quadrilateral where all the corners are on the circumference of a circle.
As before, the first step is to draw radii from the centre to each corner of the quadrilateral. This gives us four isosceles triangles: ∆ABC, ∆ACD, ∆ADE and ∆ABE.

We know that the sum of the interior angles of a quadrilateral is 360° (if you’re not sure about this, think of a square). With this, we see:
Angle B Angle C Angle D Angle E
(x+u) + (u+v) + (v+w) + (x+w) = 360°
2u + 2v + 2w + 2x = 360°
u + v + w + x = 180°
So we have:
Angle B + Angle D
(u + x) + (v + w) = 180°
and
Angle C + Angle E
(u + v) + (x + w) = 180°
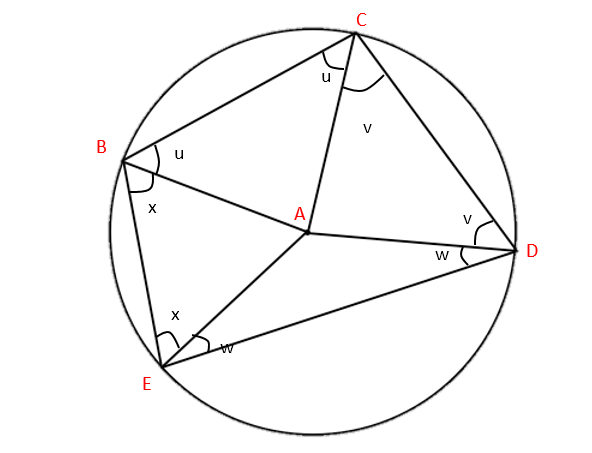
5. The angle between the chord and the tangent is equal to the angle in the alternate segment:
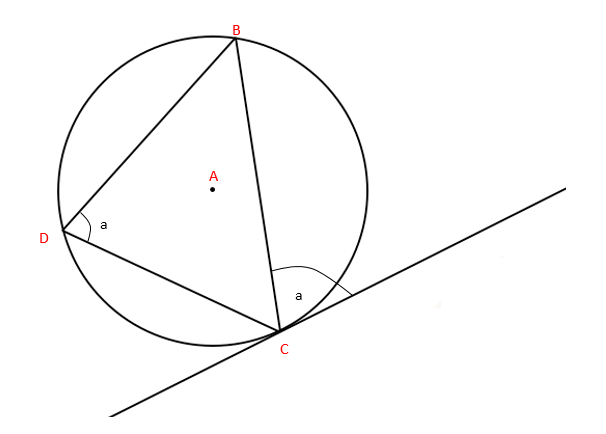

Finally, one of the more unexpected theorems we can derive from drawing lines in circles. The proof starts in the same way, by drawing radii from the centre of the circle to each of the points B, C and D.
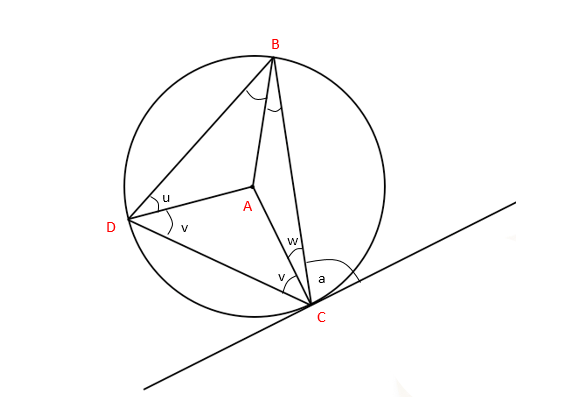

This once again forms three isosceles triangles: ∆ABC, ∆ABD and ∆ACD.
We want to show that a = u+v.
In the larger triangle ∆BCD, we know that:
(u+w) + (v+w) + (u+v) = 180° (180° in a triangle)
which leads to:
2u + 2v + 2w = 180°
u + v + w = 90° (1)
We also know that:
a = 90° – w (tangent and radius meet at 90°)
Substituting this into (1):
u + v = 90° – w
u + v = a, as required.
I think it’s remarkable what drawing a simple radius can unlock for us inside in a circle. When I learned these theorems, I never really understood where they came from – now you do!
Remember, while the questions may look complicated and it might be difficult to spot how to reach the answer, taking the time to apply these theorems will make your job a lot easier. And if you still need some help, try a one-to-one explanation from an online maths tutor.


Chris B. is studying Mathematics and Economics at University College London. He is excited by the constant challenge studying Mathematics presents, and enjoys finding new and interesting ways to solve problems.
Looking for more?
Head back to our GCSE Maths revision hub for revision guides, videos and more!




